https://www.acmicpc.net/problem/10164
10164번: 격자상의 경로
입력의 첫째 줄에는 격자의 행의 수와 열의 수를 나타내는 두 정수 N과 M(1 ≤ N, M ≤ 15), 그리고 ○로 표시된 칸의 번호를 나타내는 정수 K(K=0 또는 1 < K < N×M)가 차례로 주어지며, 각 값은 공백으
www.acmicpc.net
문제
행의 수가 N이고 열의 수가 M인 격자의 각 칸에 1부터 N×M까지의 번호가 첫 행부터 시작하여 차례로 부여되어 있다. 격자의 어떤 칸은 ○ 표시가 되어 있다. (단, 1번 칸과 N × M번 칸은 ○ 표시가 되어 있지 않다. 또한, ○ 표시가 되어 있는 칸은 최대 한 개이다. 즉, ○ 표시가 된 칸이 없을 수도 있다.)
행의 수가 3이고 열의 수가 5인 격자에서 각 칸에 번호가 1부터 차례대로 부여된 예가 아래에 있다. 이 격자에서는 8번 칸에 ○ 표시가 되어 있다.
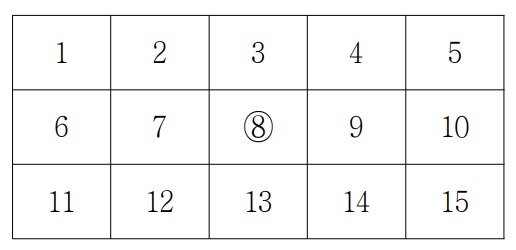
격자의 1번 칸에서 출발한 어떤 로봇이 아래의 두 조건을 만족하면서 N×M번 칸으로 가고자 한다.
- 조건 1: 로봇은 한 번에 오른쪽에 인접한 칸 또는 아래에 인접한 칸으로만 이동할 수 있다. (즉, 대각선 방향으로는 이동할 수 없다.)
- 조건 2: 격자에 ○로 표시된 칸이 있는 경우엔 로봇은 그 칸을 반드시 지나가야 한다.
위에서 보인 것과 같은 격자가 주어질 때, 로봇이 이동할 수 있는 서로 다른 경로의 두 가지 예가 아래에 있다.
- 1 → 2 → 3 → 8 → 9 → 10 → 15
- 1 → 2 → 3 → 8 → 13 → 14 → 15
격자에 관한 정보가 주어질 때 로봇이 앞에서 설명한 두 조건을 만족하면서 이동할 수 있는 서로 다른 경로가 총 몇 개나 되는지 찾는 프로그램을 작성하라.
문제접근 : (1, 1)부터 (N, M)까지의 경로 중 K위치를 지나는 경로의 경우의 수(단, K가 0일 때는 K위치를 지나는 것 고려 x) -> 동적 계획법으로 이미 진행하여 성공했던 경로는 다시 진행 하지 않고 값만 반환 받는다.
K가 0이면 K위치를 지나야한다는 조건이 없으므로 (1, 1)부터 (N, M)까지 진행하는 경우의 수 모두 체크해준다.
이것은 간단하게 메모이제이션으로 구현할 수 있고, K위치를 지나야한다는 조건이 존재할 시 조금 까다로워진다.
나는 최적부분문제 구조를 충족하기 위해 함수에 y좌표, x좌표, k를 지났는지에 대한 여부(=chk)를 매개변수로 주어
chk가 1일 경우 남은 경로 중 (N,M)까지 갈 수 있는 경우의 수를 파악해주는 방법으로 구현했다.
그리고 또 생각해야할 점이 이미 방문했었던 구역이더라도 현재 chk가 1일 때만 메모이제이션으로 저장했던 값을 반환받는 방식으로 구현했다. 이유는 chk가 0일 때도 반환받아버리면 진행해왔던 경로가 K를 지나온 경우면 달라질 수 있는 경우의 수가 존재하는데 이를 모두 무시하기 때문이다.
#include <iostream>
#include <queue>
#include <vector>
#include <stack>
#include <string>
#include <cstring>
#include <sstream>
#include <set>
#include <unordered_set>
#include <map>
#include <algorithm>
#include <cmath>
#include <ctime>
#define fastio ios::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL)
#define ENDL cout << endl
#define ll long long
#define ull unsigned long long
#define INF 987654321
#define Mod 1000000007
#define endl '\n'
using namespace std;
int N, M, K;
ll cache[17][17];
int board[17][17];
ll solution(int y, int x, int chk){
if(y > N || x > M) return 0;
if(board[y][x] == K) chk = 1;
if(y==N && x==M) {
if(chk == 1) return 1;
else return 0;
}
ll &ret = cache[y][x];
if(ret != 0 && chk == 1) return ret;
ret = 0;
return ret += (solution(y+1,x,chk) + solution(y,x+1,chk));
}
void input(){
cin >> N >> M >> K;
int p = 1;
for(int i=1;i<=N;i++){
for(int j=1;j<=M;j++){
board[i][j] = p++;
}
}
int answer;
if(K != 0) answer = solution(1, 1, 0);
else answer = solution(1, 1, 1);
cout << answer << endl;
}
int main(){
fastio;
input();
return 0;
}'BOJ > DP' 카테고리의 다른 글
| [C/C++] 백준 - 2502번 : 떡 먹는 호랑이 (0) | 2022.01.19 |
|---|---|
| [C/C++] 백준 - 11060번 : 점프 점프 (0) | 2022.01.18 |
| [C/C++] 백준 - 12014번 : 주식 (0) | 2022.01.13 |
| [C/C++] 백준 - 2011번 : 암호코드 (0) | 2022.01.12 |
| [C/C++] 백준 - 17265번 : 나의 인생에는 수학과 함께 (0) | 2021.09.25 |