https://www.acmicpc.net/problem/1725
1725번: 히스토그램
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은
www.acmicpc.net
문제
히스토그램에 대해서 알고 있는가? 히스토그램은 아래와 같은 막대그래프를 말한다.
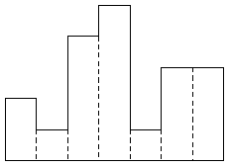
각 칸의 간격은 일정하고, 높이는 어떤 정수로 주어진다. 위 그림의 경우 높이가 각각 2 1 4 5 1 3 3이다.
이러한 히스토그램의 내부에 가장 넓이가 큰 직사각형을 그리려고 한다. 아래 그림의 빗금 친 부분이 그 예이다. 이 직사각형의 밑변은 항상 히스토그램의 아랫변에 평행하게 그려져야 한다.

주어진 히스토그램에 대해, 가장 큰 직사각형의 넓이를 구하는 프로그램을 작성하시오.
입력
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄에 가장 큰 직사각형의 넓이를 출력한다. 이 값은 20억을 넘지 않는다.
아래의 코드 및 설명은 "알고리즘 문제 해결 전략"의 일부입니다.
대표적인 분할정복 알고리즘을 이용해 풀이하는 문제이다.
분할 정복 알고리즘의 설계
분할 정복 알고리즘을 설계하기 위해서는 문제를 어떻게 분할할지를 가장 먼저 결정해야합니다.
히스토그램을 절반으로 나눠 두 개의 부분 문제를 만듭니다. 그러면 찾고자 하는 최대 직사각형은 다음 세 가지 중 하나에 속하게 됩니다.
▶ 가장 큰 직사각형을 왼쪽 부분 문제에서만 잘라낼 수 있다.
▶ 가장 큰 직사각형을 오른쪽 부분 문제에서만 잘라낼 수 있다.
▶ 가장 큰 직사각형은 왼쪽 부분 문제와 오른쪽 부분 문제에 걸쳐 있다.
이 때 첫번째와 두번째 경우는 반으로 나눈 부분 문제를 재귀 호출하여 해결할 수 있습니다.
가장 큰 직사각형의 넓이를 찾고 있기 때문에 이 중 더 큰 것을 항상 택하면 됩니다.
그리고 세 번째 경우의 답을 빠르게 구할 수만 있으면 분할 정복 알고리즘은 완성 되는 셈입니다.
양쪽 부분 문제에 걸친 경우의 답
양쪽 부분 문제에 모두 걸치는 직사각형 중 가장 큰 것을 어떻게 찾을 수 있을까?
답을 찾는 힌트는 이 직사각형은 반드시 부분 문제 경계에 있는 두 판자를 포함한다는 데 있습니다.
초기 직사각형에서 시작해 사각형을 가로로 한 칸씩 확대해 나가며 높이가 더 높은 쪽으로 포함하게끔 확장해야 면적이 넓어질 수 있습니다
시간복잡도 분석
주어진 n크기의 배열을 n/2크기의 배열 두 개로 나눈 뒤 이들을 각각 해결합니다.
재귀 호출 외에 함수 내에서 하는 일은 두 부분에 걸쳐 있는 사각형을 찾는 작업밖에 없으므로, 이 작업의 시간 복잡도가 전체 시간 복잡도를 결정합니다. 이 과정은 너비가 2인 사각형에서 시작해서 너비가 n인 사각형까지를 하나하나 검사하므로 시간복잡도는 O(n)이 됩니다.
문제를 항상 절반으로 나누어서 재귀 호출하고, O(n) 시간의 후처리를 하는 알고리즘이라고 하면 병합 정렬과 동일합니다. 이 분할 정복 아고리즘은 병합 정렬과 같은 시간복잡도 O(nlgn)을 갖습니다.
#include <iostream>
#include <queue>
#include <vector>
#include <stack>
#include <string>
#include <cstring>
#include <map>
#include <algorithm>
#include <cmath>
#define ll long long
#define INF 987654321
#define CUNLINK ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define MAX 100000 + 1
#define endl '\n'
#define pil pair<int,int>
using namespace std;
vector<int> h;
int solve(int left, int right) {
if (left == right) return h[left];
int mid = (left + right) / 2;
int ret = max(solve(left, mid), solve(mid + 1, right));
int pl = mid, pr = mid + 1;
int height = min(h[pl], h[pr]);
ret = max(ret, height * 2);
while (left < pl || pr < right) {
if (pr < right && (pl == left || h[pl - 1] < h[pr + 1])) {
++pr;
height = min(height, h[pr]);
}
else {
--pl;
height = min(height, h[pl]);
}
ret = max(ret, height * (pr - pl + 1));
}
return ret;
}
int main() {
CUNLINK;
int N; cin >> N;
for (int i = 0; i < N; i++) {
int x; cin >> x;
h.push_back(x);
}
cout << solve(0, h.size() - 1);
return 0;
}
'BOJ > 분할정복' 카테고리의 다른 글
| [C/C++] 백준 - 13171번 : A (0) | 2022.05.18 |
|---|---|
| [C/C++] 백준 - 2630번 : 색종이 만들기 (0) | 2022.02.25 |
| [C/C++] 백준 - 10830번 : 행렬 제곱 (0) | 2022.01.10 |
| [C/C++] 백준 - 1780번 : 종이의 개수 (0) | 2021.09.24 |
| [C/C++] 백준 - 1992번 : 쿼드 트리 (0) | 2021.09.09 |