https://www.acmicpc.net/problem/16947
16947번: 서울 지하철 2호선
첫째 줄에 역의 개수 N(3 ≤ N ≤ 3,000)이 주어진다. 둘째 줄부터 N개의 줄에는 역과 역을 연결하는 구간의 정보가 주어진다. 같은 구간이 여러 번 주어지는 경우는 없고, 역은 1번부터 N번까지 번호
www.acmicpc.net
문제
서울 지하철 2호선은 다음과 같이 생겼다.
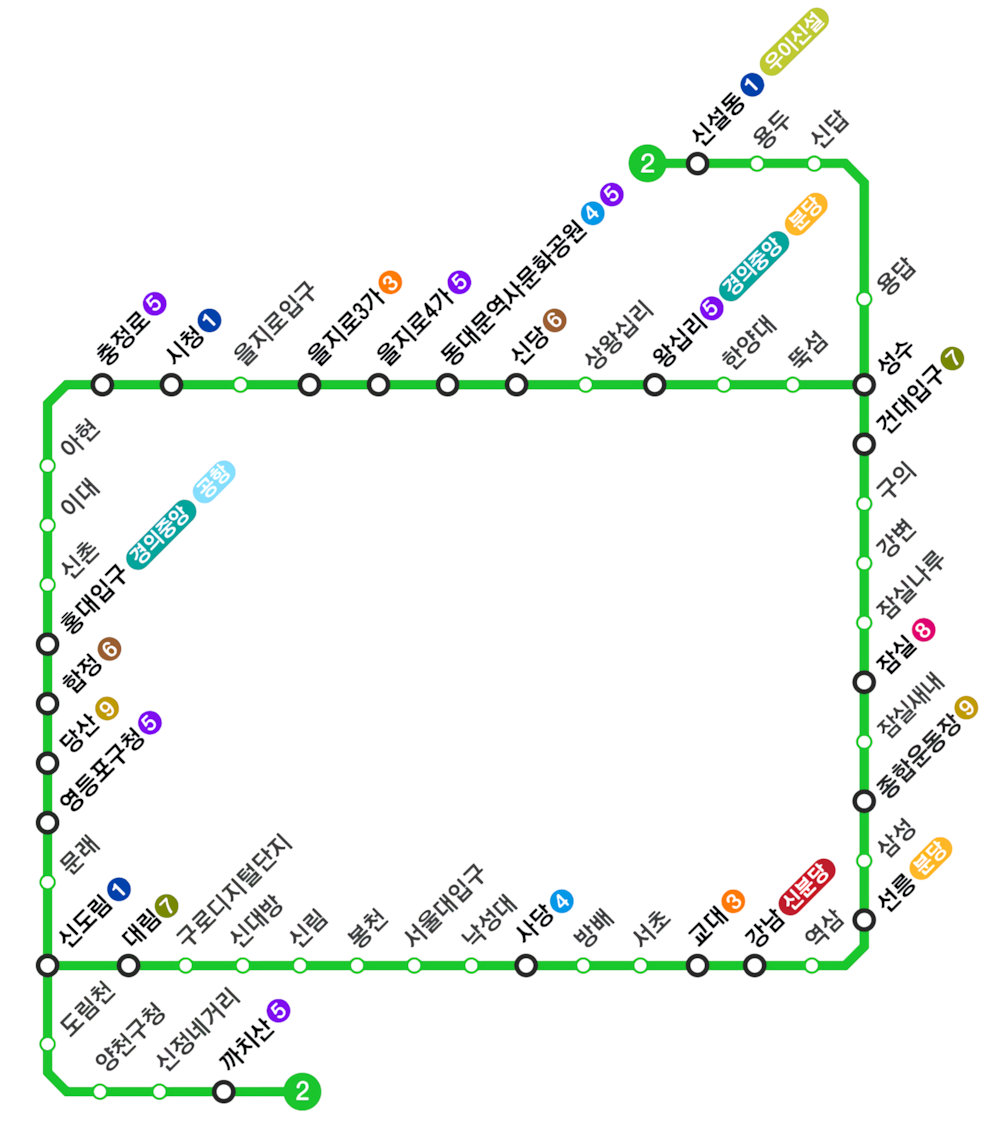
지하철 2호선에는 51개의 역이 있고, 역과 역 사이를 연결하는 구간이 51개 있다. 즉, 정점이 51개이고, 양방향 간선이 51개인 그래프로 나타낼 수 있다. 2호선은 순환선 1개와 2개의 지선으로 이루어져 있다. 한 역에서 출발해서 계속 가면 다시 출발한 역으로 돌아올 수 있는 노선을 순환선이라고 한다. 지선은 순환선에 속하는 한 역에서 시작하는 트리 형태의 노선이다.
두 역(정점) 사이의 거리는 지나야 하는 구간(간선)의 개수이다. 역 A와 순환선 사이의 거리는 A와 순환선에 속하는 역 사이의 거리 중 최솟값이다.
지하철 2호선과 같은 형태의 노선도가 주어졌을 때, 각 역과 순환선 사이의 거리를 구해보자.
입력
첫째 줄에 역의 개수 N(3 ≤ N ≤ 3,000)이 주어진다. 둘째 줄부터 N개의 줄에는 역과 역을 연결하는 구간의 정보가 주어진다. 같은 구간이 여러 번 주어지는 경우는 없고, 역은 1번부터 N번까지 번호가 매겨져 있다. 임의의 두 역 사이에 경로가 항상 존재하는 노선만 입력으로 주어진다.
출력
총 N개의 정수를 출력한다. 1번 역과 순환선 사이의 거리, 2번 역과 순환선 사이의 거리, ..., N번 역과 순환선 사이의 거리를 공백으로 구분해 출력한다.
쉽지 않았던 문제이다.
이 문제의 핵심은 "무방향 그래프에서 순환 찾기" 이다.
역의 개수가 크지 않고 간선의 개수도 역의 개수보다 작으므로 완전탐색을 이용해 구할 수 있다.
먼저 거리를 저장해줄 배열을 모두 -1로 초기화 해준다. 이유는 순환 그래프의 거리는 0이 될 것이고, 비순환 그래프에서 순환그래프까지의 거리가 1이 될 수도 있으므로 존재할 수 없는 값인 -1로 초기화해주는 것이다.
1. 모든 노드를 시작지점으로 완전탐색을 진행하며 순환 그래프인지 확인한다.
2. 순환 그래프라면 거리를 0으로 초기화 해주고 순환 그래프가 아니라면 큐에 넣어준다.
위 1,2번을 N번 노드까지 반복문을 통해 확인하면 순환 그래프는 거리 배열에 0으로 초기화가 될 것이고, 비순환 그래프는 큐에 담길 것이다.
여기서 주의해야 할 점이, 이 문제에서 순환 그래프라 함은, N번 노드에서 출발하여 N번노드까지 제자리로 돌아오는 것을 의미한다. 이 부분을 놓쳐 디버깅이 오래 걸렸다.
이제 위 과정으로 순환 그래프의 거리를 0으로 모두 초기화 해주었고, 큐에 담겨있는 비순환 그래프에 포함되는 노드들을 순환 그래프까지의 거리를 구해주어야한다. 이 부분은 DFS로 쉽게 구현할 수 있다.
#include <iostream>
#include <list>
#include <queue>
#include <stack>
#include <string>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <cmath>
#include <bitset>
#define INF 987654321
#define Mod 9901
#define CUNLINK ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
#define ll long long
#define ENDL cout << endl
#define endl '\n'
using namespace std;
typedef struct GraphNode {
int cost;
int dest;
GraphNode* next;
}GraphNode;
typedef struct Graph {
int cnt;
GraphNode* adj;
}Graph;
int N;
int visited[3001];
bool visited2[3001];
int dist[3001];
bool isEnd = false;
void Init_Graph(Graph* gph, int cnt) {
gph->cnt = cnt;
gph->adj = (GraphNode*)malloc(sizeof(GraphNode) * (cnt+1));
for (int i = 1; i <= cnt; i++) gph->adj[i].next = NULL;
}
int AddDirectedLinkedEdge(Graph* gph, int src, int dst, int cost) {
GraphNode* Temp = (GraphNode*)malloc(sizeof(GraphNode));
Temp->cost = cost;
Temp->dest = dst;
Temp->next = gph->adj[src].next;
gph->adj[src].next = Temp;
return 1;
}
int AddUnDirectedLinkedEdge(Graph* gph, int src, int dst, int cost) {
return AddDirectedLinkedEdge(gph, src, dst, cost) && AddDirectedLinkedEdge(gph, dst, src, cost);
}
int isCyclePresentUnDirectedEdge(Graph* gph, int start, int index, int prev) {
visited[index] = 1;
GraphNode* head = gph->adj[index].next;
while (head) {
if (!visited[head->dest]) {
if (isCyclePresentUnDirectedEdge(gph, start, head->dest, index))
return 1;
}
else if (head->dest != prev && head->dest == start)
return 1;
head = head->next;
}
visited[index] = 2;
return 0;
}
void DFS(Graph* gph, int Init, int index, int len) {
visited2[index] = true;
GraphNode* head = gph->adj[index].next;
while (head) {
if (!visited2[head->dest]) {
if (dist[head->dest] == 0) {
isEnd = true;
dist[Init] = len + 1;
return;
}
else {
DFS(gph, Init, head->dest, len + 1);
if (isEnd) break;
}
}
head = head->next;
}
}
int main() {
CUNLINK;
Graph graph;
queue<int> q;
cin >> N;
Init_Graph(&graph, N);
memset(dist, -1, sizeof(dist));
for (int i = 0; i < N; i++) {
int a, b;
cin >> a >> b;
AddUnDirectedLinkedEdge(&graph, a, b, 1);
}
for (int i = 1; i <= N; i++) {
memset(visited, false, sizeof(visited));
if (!visited[i]) {
if (isCyclePresentUnDirectedEdge(&graph, i, i, -1)) {
dist[i] = 0;
}
else {
q.push(i);
}
}
}
while (!q.empty()) {
int y = q.front(); q.pop();
isEnd = false;
DFS(&graph, y, y, 0);
memset(visited2, false, sizeof(visited2));
}
for (int i = 1; i <= N; i++)
cout << dist[i] << " ";
return 0;
}
'BOJ > 그래프 이론' 카테고리의 다른 글
| [C/C++] 백준 - 1865번 : 웜홀 (벨만포드) (0) | 2021.09.04 |
|---|---|
| [C/C++] 백준 - 1707번 : 이분 그래프 (0) | 2021.09.03 |
| [C/C++] 백준 - 11657번 : 타임머신 (벨만 포드) (0) | 2021.09.01 |
| [C/C++] 백준 - 2150번 : Strongly Connected Component (SCC Algorithm) (0) | 2021.08.26 |
| [C/C++] 백준 - 14621번 : 나만 안되는 연애 (0) | 2021.08.26 |