▶ 명제 지식베이스 : PropKB
PropKB 클래스는 명제 논리 문장의 지식 베이스를 나타내는 데 사용할 수 있습니다.
KB 클래스에는 __init__ 메서드 외에 네 가지 메서드가 있습니다. 여기서 주목할 점은 ask 메서드가 단순히 ask_generator 메서드를 호출하기 때문에 직접 지식 베이스 클래스를 만들 때 실제로 구현해야 할 것은 ask 함수 자체가 아니라 ask_generator 함수일 것입니다.
init(self, sentence=None): 생성자 __init__은 하나의 필드 clauses를 생성합니다. 이 필드는 지식 베이스의 모든 문장을 나타내는 리스트입니다. 이 중 각각의 문장은 '절(clause)'이 됩니다. 즉, 리터럴(literal)과 논리합(or)만으로 이루어진 문장입니다.
tell(self, sentence): 지식 베이스에 문장을 추가하려면 tell 메서드를 사용합니다. 이 메서드는 문장을 가져와 CNF로 변환하고 모든 절을 추출하여 clauses 필드에 추가합니다. 따라서 지식 베이스에 절만 추가해야한다는 걱정은 하지 않아도 됩니다. 원하는 형태의 문장을 지식 베이스에 알리고, tell 메서드가 CNF로 변환하고 그 결과의 절을 추가하는 일을 처리합니다.
ask_generator(self, query): ask 함수에서 사용되는 ask_generator 함수입니다. 이 함수는 tt_entails 함수를 호출합니다. 이 함수는 지식 베이스가 query를 함의하는 경우 True를 반환하고, 그렇지 않은 경우 False를 반환합니다. ask_generator 함수 자체는 지식 베이스가 query를 함의하는 경우 빈 dict {}를 반환하고, 그렇지 않은 경우 None을 반환합니다. 이렇게 하는 이유는 일차 논리(First-Order Logic)에서 ask_generator 함수가 query를 참으로 만드는 모든 대체 값을 반환해야하기 때문입니다. 따라서 모든 대체 값을 반환하기 위해 dict를 사용하는 것입니다. 대부분 ask 함수를 사용할 것이며, 이 함수는 {} 또는 False를 반환합니다. 그러나 이게 마음에 들지 않으면 True나 False를 반환하는 ask_if_true 함수를 사용할 수 있습니다.
retract(self, sentence): 이 함수는 지식 베이스에서 주어진 문장의 모든 절을 제거합니다. tell 함수와 마찬가지로 지식 베이스에서 제거할 절을 전달할 필요는 없습니다. 어떤 문장이든지 괜찮습니다. 이 함수가 해당 문장을 절로 변환하고 그것을 제거하는 일을 처리합니다.
CNF란 Conjunctive Normal Form의 약자로, 일반적인 논리식을 일정한 형태로 변환한 것입니다.
논리식을 CNF로 변환하면, 논리식을 AND 연산자로 연결된 일련의 절(clause)의 형태로 나타낼 수 있습니다. 이 때, 각 절은 OR 연산자로 연결된 리터럴(literal)의 집합으로 이루어져 있습니다. 즉, CNF는 AND 연산자와 OR 연산자만을 사용하는 논리식으로, 각각의 절은 OR 연산자로 결합되고, 각각의 절 내부의 리터럴들은 AND 연산자로 결합되는 형태를 가지게 됩니다.
▶ 지식 베이스
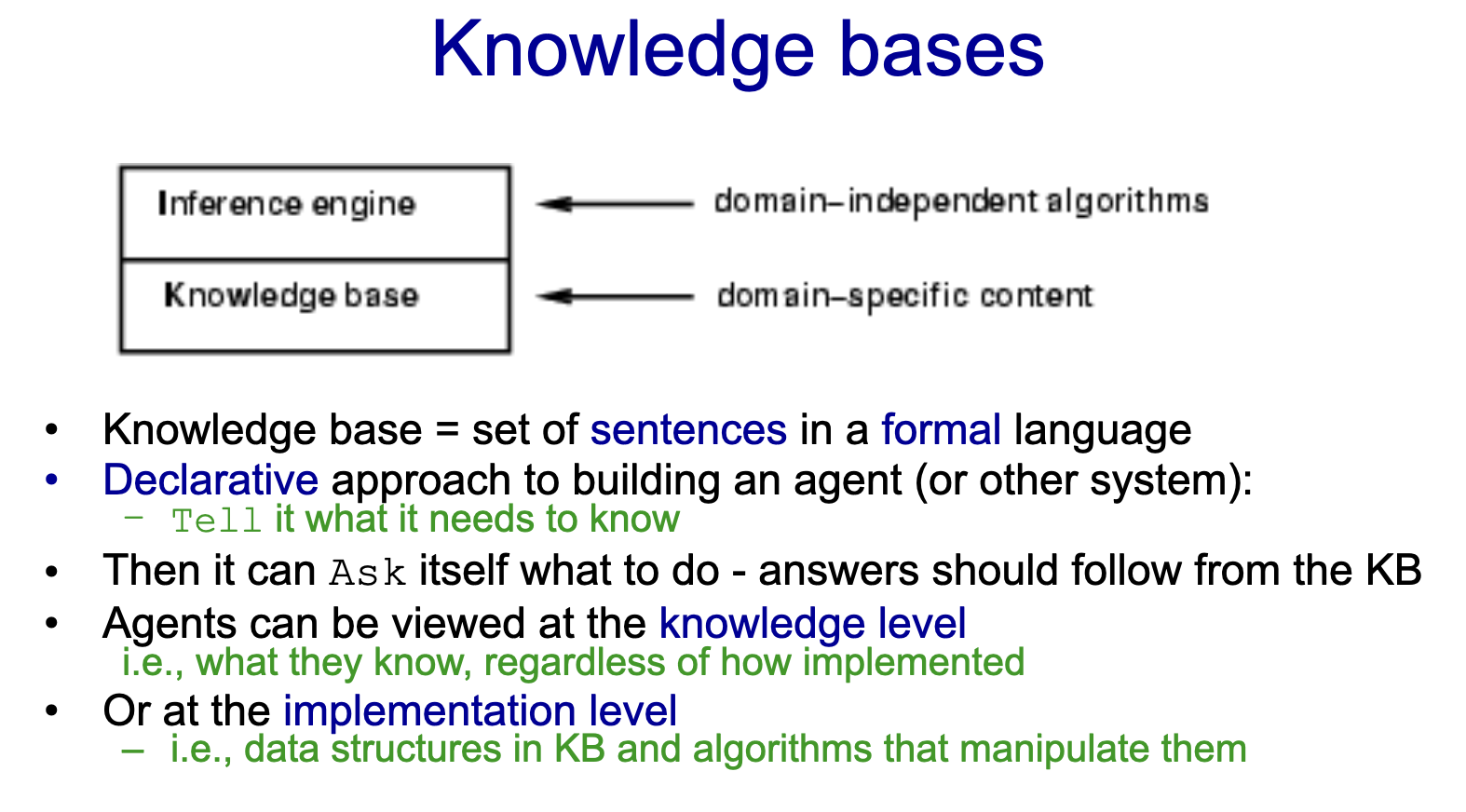
지식 베이스는 크게 두 가지 액션
1. 새 문장 추가 - Tell
2. 문장 질의 - Ask
모든 agents들은 지각 하나 입력, 동작 하나 반환.
1. 호출
2. 지식 베이스에 tell
3. 자기가 해야할 것은 지식 베이스에 ask
4. Agents는 자신이 선택한 행동을 지식 베이스에 알려줌 동작할 수 있도록
▶ 지식 베이스 Sudo Code

위 4가지 순서처럼
1. Make-Percept-Sentence
2. Make-Action-Query
3. Make-Action-Sentence
4. return Action
▶ Wumpus World 예시를 통한 이해

여러 가지 통로로 연결되어있고 자기 방으로 들어오면 먹을 수 있는 괴물 = Wumpus
화살 하나로 죽일 수 있음. 어떤 방에는 구덩이가 있고 빠지면 빠져나올 수 없음. Wumpus는 구덩이보다 커서 안빠짐
금덩이가 모인 방이 있고 결론적으로 금을 가지고 빠져나오면 +1000, 빠지면 -1000, 동작 하나에 -1, 화살 쏘는데 -10
동작들
1. 좌회전, 우회전, 직진, 금덩이 줍는 Grab, Wumbus를 향해 화살 쏘는 Shoot
하나의 Cell에서 5가지 Sensor
Agents는 구덩이 인접한 칸에서 미풍
Wumpus근처에서 Stench를 느낌
CNF란 Conjunctive Normal Form의 약자로, 일반적인 논리식을 일정한 형태로 변환한 것입니다.
논리식을 CNF로 변환하면, 논리식을 AND 연산자로 연결된 일련의 절(clause)의 형태로 나타낼 수 있습니다. 이 때, 각 절은 OR 연산자로 연결된 리터럴(literal)의 집합으로 이루어져 있습니다. 즉, CNF는 AND 연산자와 OR 연산자만을 사용하는 논리식으로, 각각의 절은 OR 연산자로 결합되고, 각각의 절 내부의 리터럴들은 AND 연산자로 결합되는 형태를 가지게 됩니다.
▶ 이것들을 지식 베이스로 표현 (아래 두 가지 사진이 동일한 것을 의미)


▶ 추론 절차

KB가 문장 알파를 함축(entail)
▶ Entailment

KB가 문장 a(알파)를 함축한다. KB가 참으로 성립해야 알파 또한 참으로 성립
▶ 코드로 표현

심볼이 정의된 경우, 이 루틴은 심볼의 모든 진리값 조합을 재귀적으로 구성하고, 그런 다음 해당 모델이 KB와 일치하는지 확인합니다. 주어진 모델은 진리표의 각 행에 해당하며, 이러한 행에 대해 KB 열에 'true'가 있으며 이 열에 대해 쿼리가 참인지 확인합니다.
즉, tt_check_all은 각 모델에 대해 이 논리식을 계산합니다.
pl_true(kb, model) => pl_true(alpha, model)
이는 논리적으로 동등한 다음 논리식과 같습니다.
pl_true(kb, model) & ~pl_true(alpha, model)
즉, 지식 베이스와 쿼리의 부정이 논리적으로 일관되지 않습니다.
tt_entails() 함수는 쿼리에서 심볼을 추출하고 적절한 매개변수로 tt_check_all() 함수를 호출합니다.
→ 하나의 문장, 정의에 따라 다른 하나의 문장에 함축되는지 확인하는 Method
▶ 예시
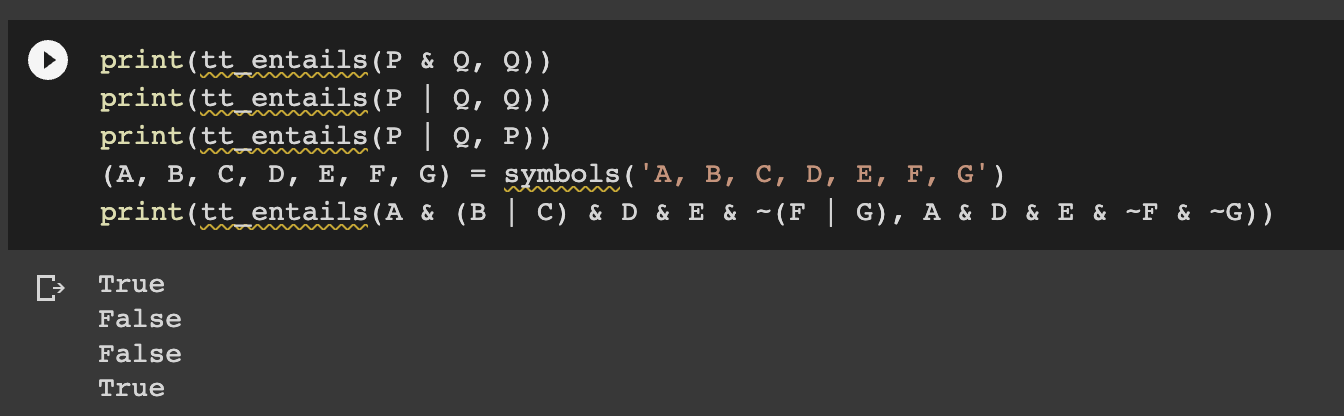
첫 번째 문장으로 예를 들어보면 P & Q가 Q에 함축적으로 성립하는지에 따라 True, False
▶ 분해 증명 : 알고리즘이 완결적인지 판단하는 방법
그러나, resolution을 통한 증명을 구현하는 알고리즘은 복잡한 문장을 처리할 수 없습니다. 따라서, 함의 연산과 이중 함의 연산은 더 단순한 절(clauses)으로 단순화되어야 합니다. 우리는 이미 모든 명제 논리 문장이 절의 연결(disjunction)로 표현 가능함을 알고 있습니다. 이 사실을 우리의 이점으로 활용하기 위해, 입력 문장을 연접 정규형(CNF, Conjunctive Normal Form)으로 단순화할 것입니다. 이는, 문자의 연결로 이루어진 교집합입니다. 예를 들어,
이는 디지털 전자에서의 합의 곱(Product of sums) 형태와 동일합니다.
이러한 변환의 개요는 다음과 같습니다.
- 이중 함의 연산을 함의 연산으로 변환합니다.
𝛼⟺𝛽는 (𝛼⟹𝛽)∧(𝛽⟹𝛼)로 작성할 수 있습니다.
이것은 복합 문장에도 적용됩니다.
𝛼⟺(𝛽∨𝛾)는 (𝛼⟹(𝛽∨𝛾))∧((𝛽∨𝛾)⟹𝛼)로 작성할 수 있습니다. - 함의 연산을 논리적으로 등가한 식으로 변환합니다.
𝛼⟹𝛽는 ¬𝛼∨𝛽로 작성할 수 있습니다. - 부정을 내부로 이동합니다.
CNF는 원자적인 리터럴만 허용합니다. 그래서 부정은 복합문장에 나타낼 수 없습니다. De Morgan의 법칙이 여기서 도움이 됩니다.
¬(𝛼∧𝛽)≡(¬𝛼∨¬𝛽)
¬(𝛼∨𝛽)≡(¬𝛼∧¬𝛽) - 분배 법칙을 사용하여 합집합과 교집합을 분배합니다.
합집합과 교집합은 서로 분배될 수 있습니다. 이제 우리는 절의 연결, 합집합 및 부정만 가진 문장을 가지고 있습니다. 따라서 가능한 한 합집합을 분배하여 더 단순한 절의 연결로 이루어진 문장을 얻습니다.
우리는 다음과 같은 형태를 필요로 합니다.
(𝛼1∨𝛼2∨𝛼3...)∧(𝛽1∨𝛽2∨𝛽3...)∧(𝛾1∨𝛾2∨𝛾3...)∧...
3줄 요약
1. 절로 단순화
2. 연결료 표현
3. 정규형(CNF로 단순화)
▶ 분해 증명 코드로 나타내는 방법
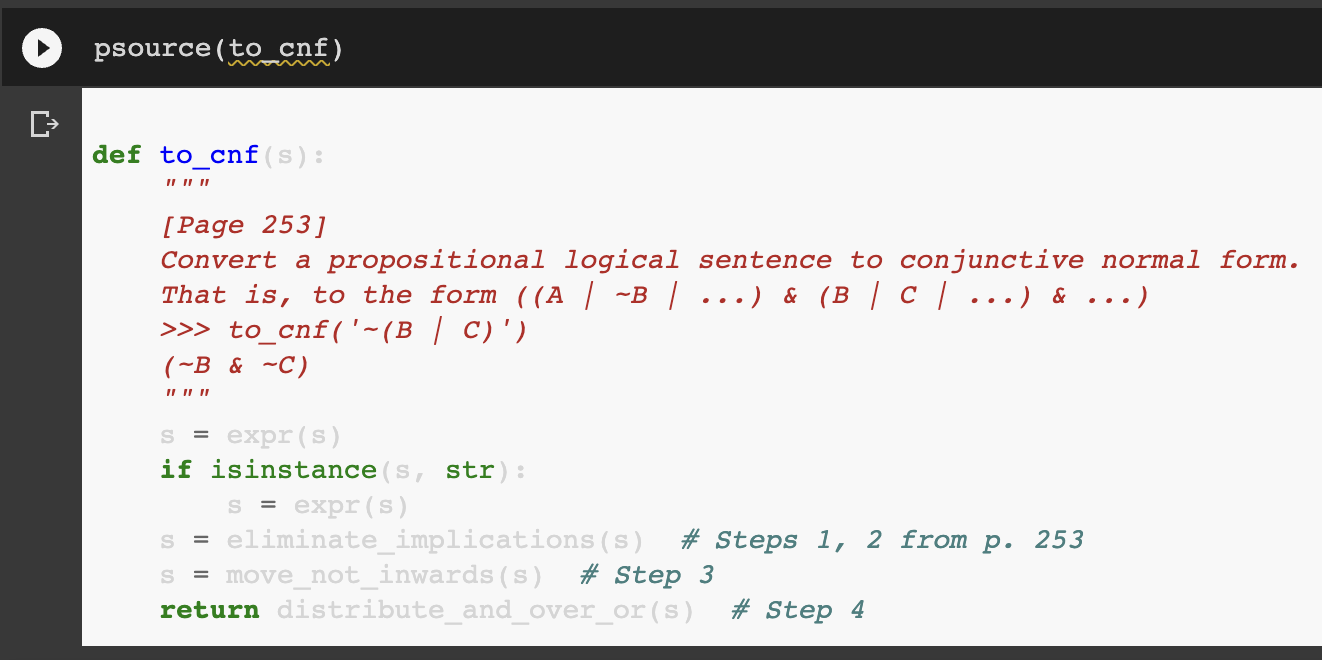
to_cnf함수는 세 개의 하위 루틴을 호출한다.
- eliminate_implications는 바이-임플리케이션과 임플리케이션을 논리적 등가물로 변환한다.
- move_not_inwards는 합성 명제에서 부정을 제거하고 De Morgan의 법칙을 사용하여 내부로 이동한다.
- distribute_and_over_or는 합연산자를 교환법칙을 이용하여 분배
[3가지 루틴의 대한 코드]



조금 더 과정을 자세하게 나타내는 코드 : 내부적으로 이해해야 중간고사든 과제든 수행할 수 있음 씌벌
▶ 분해 증명 예시 코드

▶ 절의 표현 (이론 수업에서 아직 안함, 간단한 개념만 설명)
분해를 지금까지 했는데 분해증명을 통해 완결성 있는 추론을 진행
실제에서는 분해를 모두 할 필요 없고 일부만 필요
제한적이고 효율적인 알고리즘을 적용할 수 있다. 분해 증명이 좋지만 조금 더 효율적인 방법이 뭘까? 고민해서 적용할 수 있는 3개의 절
▶ 순방향과 역방향 연쇄
이전에 우리는 KB에 의해 entail되는 문장을 확인하기 위해 두 가지 알고리즘을 살펴볼 것이라고 말했습니다. 여기에 세 번째 알고리즘이 있습니다. 다른 점은 지식 베이스에서 확실한 절만 포함하고 있는 경우에 한해서, 단일 명제 기호 q가 entail되는지를 결정하는 것입니다. 그러나 뭔가 주의해야 할 점이 있습니다. 지식 베이스는 반드시 Horn 절(clause)만 포함해야 합니다.
Horn 절(clause) Horn 절은 최대한 하나의 양의 리터럴로 구성된 리터럴의 합집합으로 정의할 수 있습니다.
정확히 하나의 양의 리터럴을 가지는 Horn 절을 확실한 절(definite clause)이라고 합니다.
Horn 절은 다음과 같이 생겼을 수 있습니다.
¬𝑎∨¬𝑏∨¬𝑐∨¬𝑑...∨𝑧
그러나 이 예시 또한 확실한 절입니다.
De Morgan의 법칙을 이용하면, 위의 예시를 다음과 같이 단순화할 수 있습니다.
𝑎∧𝑏∧𝑐∧𝑑...⟹𝑧
이것은 인간이 알고 있는 데이터와 사실을 처리하는 논리적인 표현처럼 보입니다. 감지된(percepts) a, b, c, d ... 가 동시에 참이라고 가정하면, 그 시점에서 z도 참일 것이라는 것을 추론할 수 있습니다. 알고리즘적으로 추론 또는 해결(resolution)을 더 쉽게 만드는 Horn 절의 몇 가지 흥미로운 측면이 있습니다.
- 확실한 절은 함축(implication)로 작성될 수 있습니다:
확실한 절에서 가장 중요한 단순화는 함축으로 작성될 수 있다는 것입니다. 전제(또는 함축에 이르는 지식)는 양의 리터럴의 연결(conjunction)입니다. 결론(시사하는 문장) 또한 양의 리터럴입니다. 문장은 이제 이해하기 쉬워졌습니다. 전제와 결론은 관례적으로 body와 head라고 불립니다. 하나의 양의 리터럴은 fact이라고 합니다. - Horn 절에서 전방 추론 및 후방 추론을 추론에 사용할 수 있습니다
전진 연쇄는 검색 알고리즘 장에서 소개한 `AND-OR-Graph-Search`와 의미론적으로 동일합니다. 구현 세부 정보는 곧 설명하겠습니다. - Horn 절을 사용하여 간단하게 entailment 결정 가능:
놀랍게도, 전진 및 후진 연쇄 알고리즘은 지식 베이스의 각 요소를 최대 한 번만 탐색하므로 문제를 크게 단순화합니다.
함수 `pl_fc_entails`은 전진 연쇄를 구현하여 지식 베이스 `KB`가 심볼 `q`를 entail하는지 확인합니다.
그러나, `pl_fc_entails`은 보통의 `KB` 인스턴스를 사용하지 않습니다. 여기서 지식 베이스는 `PropKB` 클래스에서 파생된 `PropDefiniteKB` 클래스의 인스턴스이지만, 수정하여 결정적인 절을 저장하도록 변경되었습니다.
주요 차이점은 주어진 심볼 `p`를 premise에 가진 KB 절의 목록을 반환하는 `PropDefiniteKB`에 대한 도우미 메소드의 포함입니다.
추론을 수행할 때 순방향, 역방향 연쇄 알고리즘을 사용한다는 것
※ 절의 표현부터는 이론 수업에서 다시 들어야 하는 부분
'2023 > 2023-1' 카테고리의 다른 글
| [4월4일(화)] 인공지능 입문(이론) - Introduction to Machine Learning (0) | 2023.04.04 |
|---|---|
| [3월30일(목)] 인공지능 입문(실습) - 확률 이론 (0) | 2023.03.30 |
| [캡스톤디자인] 제안서 발표 피드백 정리 (0) | 2023.03.24 |
| [3/21(화)] 인공지능 입문(이론) - 명제 지식 베이스, 진리표(과제 있음) (0) | 2023.03.21 |
| 2023년 캡스톤 디자인 정보통신공학과 졸업 프로젝트 (0) | 2023.03.18 |