1. 확률 분포
확률 분포란, 확률 변수가 가질 수 있는 각각의 값에 어떤 확률이 배정되는 지를 결정한다. 이번 실습에서는 이런 확률 변수를 쉽게 정의하고 나타낼 수 있는 클래스를 활용하여 다양한 경우를 탐색해보고자 한다.
우선, ProbDist 클래스를 통해서 이산 확률 분포를 지정해보자. 랜덤 변수의 이름을 지정한 다음 확률을 할당할 수 있다. 딕셔너리와 유사하게 생각하면 된다.
psource(ProbDist)class ProbDist:
"""A discrete probability distribution. You name the random variable
in the constructor, then assign and query probability of values.
>>> P = ProbDist('Flip'); P['H'], P['T'] = 0.25, 0.75; P['H']
0.25
>>> P = ProbDist('X', {'lo': 125, 'med': 375, 'hi': 500})
>>> P['lo'], P['med'], P['hi']
(0.125, 0.375, 0.5)
"""
def __init__(self, var_name='?', freq=None):
"""If freq is given, it is a dictionary of values - frequency pairs,
then ProbDist is normalized."""
self.prob = {}
self.var_name = var_name
self.values = []
if freq:
for (v, p) in freq.items():
self[v] = p
self.normalize()
def __getitem__(self, val):
"""Given a value, return P(value)."""
try:
return self.prob[val]
except KeyError:
return 0
def __setitem__(self, val, p):
"""Set P(val) = p."""
if val not in self.values:
self.values.append(val)
self.prob[val] = p
def normalize(self):
"""Make sure the probabilities of all values sum to 1.
Returns the normalized distribution.
Raises a ZeroDivisionError if the sum of the values is 0."""
total = sum(self.prob.values())
if not np.isclose(total, 1.0):
for val in self.prob:
self.prob[val] /= total
return self
def show_approx(self, numfmt='{:.3g}'):
"""Show the probabilities rounded and sorted by key, for the
sake of portable doctests."""
return ', '.join([('{}: ' + numfmt).format(v, p) for (v, p) in sorted(self.prob.items())])
def __repr__(self):
return "P({})".format(self.var_name)
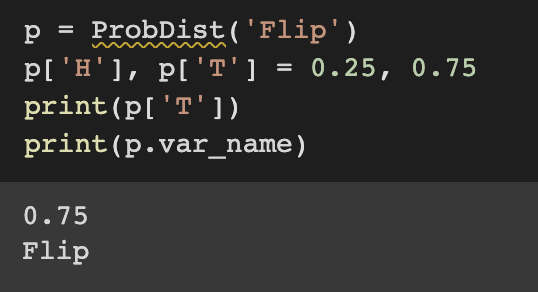
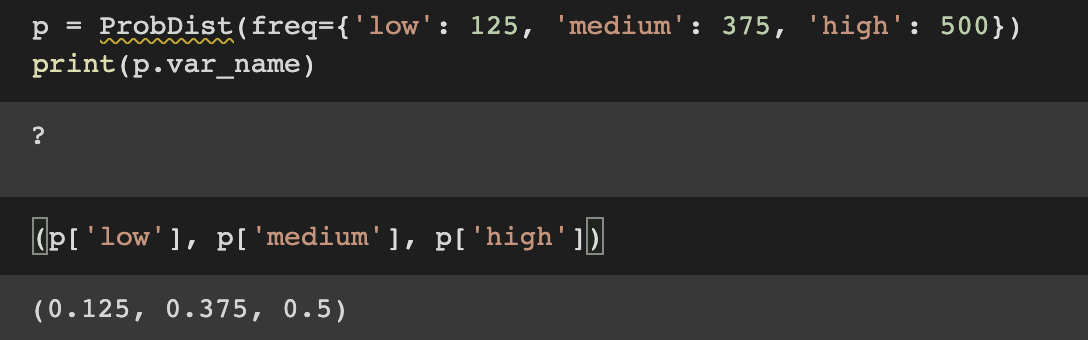
varname을 지정해주지 않으면 ? 로 기본설정된다. freqs를 통해서 딕셔너리 형태로 {랜덤 변수 : 확률}의 형태로 클래스를 정의할 수 있다. 그리고 확률란에 value로 입력된 값들을 모두 normalized되어 입력된 모든 value들의 합이 1인 형태로 자동 정규화된다
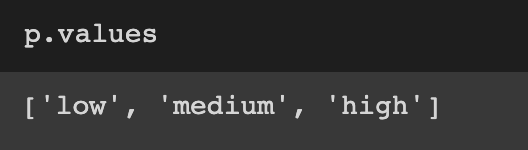
확률 분포 내의 모든 값을 개별적으로도 확인할 수 있다. 즉, unique한 랜덤 변수들의 값을 values를 통해서 확인할 수 있으며 이는 __setitem__ 메서드에서 확인 가능하다
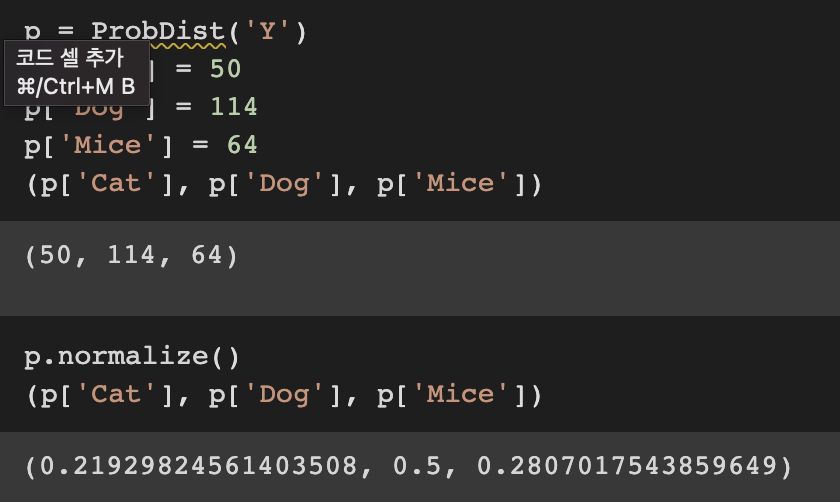
값들이 한번에 입력되면 자동으로 정규화를 진행하지만, 그렇지 않고 하나씩 값이 추가되면 자동으로 정규화를 하지 않는 문제가 있다. 이는 normalize 메서드를 활용하여 해결할 수 있다.
근사 값을 show_approx 메서드를 통해 보기 좋게 확인할 수 있다.

2. 결합 확률 분포
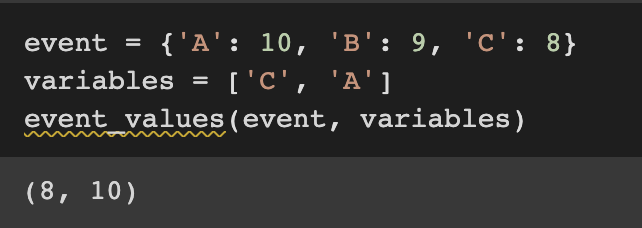
event_values 함수는 사건에 있는 변수 값의 튜플을 반환합니다. 하나의 사건은 딕셔너리로 지정됩니다. 여기서 key는 변수의 이름이고 값은 변수의 값입니다. 변수는 list와 함께 지정됩니다. 반환된 튜플의 순서는 변수의 순서와 동일합니다.
확률 변수는 모든 랜덤 변수에 대한 결합 확률 분포로서 완전하게 결정됩니다. 확륙 모듈은 이를 JointProbDist라는 클래스를 통해서 구현합니다. 이 클래스는 변수 집합에 대한 이산 확률 분포를 지정합니다.
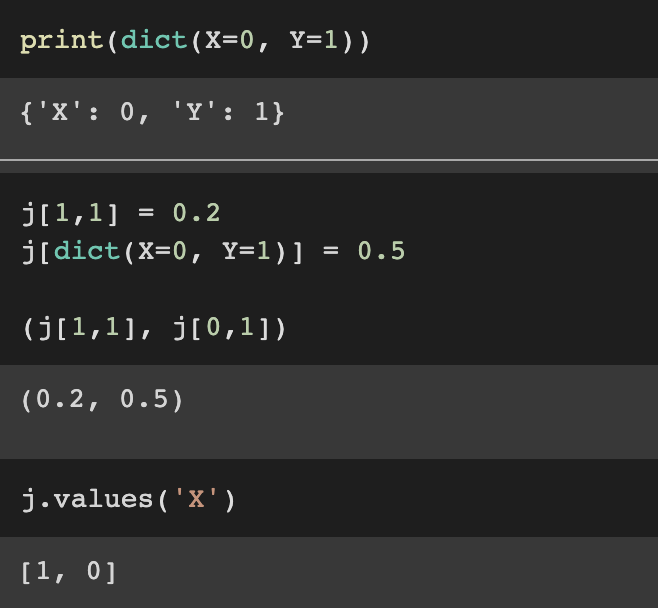
psource(JointProbDist)class JointProbDist(ProbDist):
"""A discrete probability distribute over a set of variables.
>>> P = JointProbDist(['X', 'Y']); P[1, 1] = 0.25
>>> P[1, 1]
0.25
>>> P[dict(X=0, Y=1)] = 0.5
>>> P[dict(X=0, Y=1)]
0.5"""
def __init__(self, variables):
self.prob = {}
self.variables = variables
self.vals = defaultdict(list)
def __getitem__(self, values):
"""Given a tuple or dict of values, return P(values)."""
values = event_values(values, self.variables)
return ProbDist.__getitem__(self, values)
def __setitem__(self, values, p):
"""Set P(values) = p. Values can be a tuple or a dict; it must
have a value for each of the variables in the joint. Also keep track
of the values we have seen so far for each variable."""
values = event_values(values, self.variables)
self.prob[values] = p
for var, val in zip(self.variables, values):
if val not in self.vals[var]:
self.vals[var].append(val)
def values(self, var):
"""Return the set of possible values for a variable."""
return self.vals[var]
def __repr__(self):
return "P({})".format(self.variables)결합 분포에 대한 값은 각 항목이 특정 변수와 연관된 값에 해당하는 순서가 지정된 튜플입니다. X, Y의 결합 분포의 경우, X와 Y는 정수값을 취합니다. 예를들어 (18, 19). 결합 분포를 구체화하기 위해서는 우선 변수들의 list가 필요합니다.

ProbDist 클래스처럼 JointProbDist 클래스는 서로 다른 값에 대해 확률을 할당합니다. 분포의 가능한 모든 값에 대해서 두가지 형식으로 정의될 수 있습니다.
3. 완전 결합 분포를 활용한 추론
확률적 추론을 수행하는, 다시 말해 관측된 증거가 주어졌을 때 질의(query) 명제로부터 사후 확률들을 계산하는 방법을 설명한다. 이를 파이썬 딕셔너리를 사용하여 표현한다. 아래의 식은 수업시간에 다룬 식이다.
여기서 α 는 정규화 상수를, X는 질의 변수, e는 증거 변수들의 관측된 값들의 목록, Y를 관측되지 않은 변수들의 목록이라고 할때 이 Y 집합의 값들의 모든 가능한 조합을 y를 의미한다고 하자.
그리고 이를 확인하기 위해 수업시간에 사용하였던 아래의 예제를 구현해보자
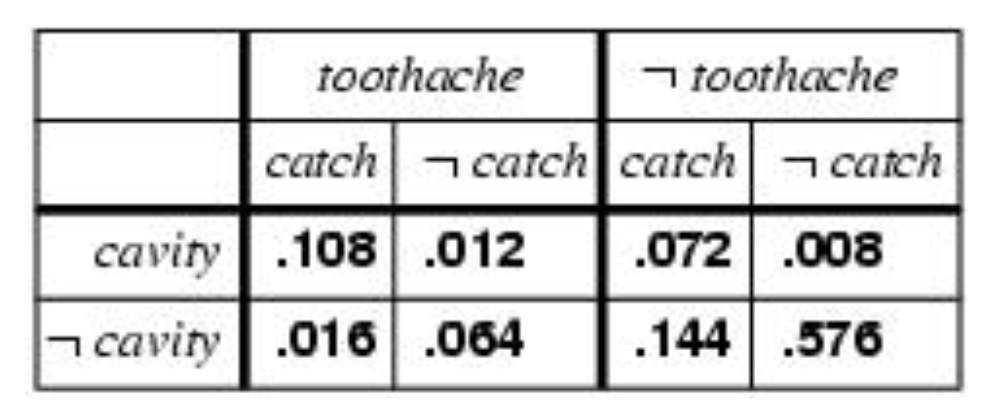

psource(enumerate_joint)def enumerate_joint(variables, e, P):
"""Return the sum of those entries in P consistent with e,
provided variables is P's remaining variables (the ones not in e)."""
if not variables:
return P[e]
Y, rest = variables[0], variables[1:]
return sum([enumerate_joint(rest, extend(e, Y, y), P) for y in P.values(Y)])P(toothache = True)를 찾고 싶다고 가정하자. 이는 marginalization을 통해서 얻을 수 있다. enumerate_joint를 통해서 이를 구해보자.

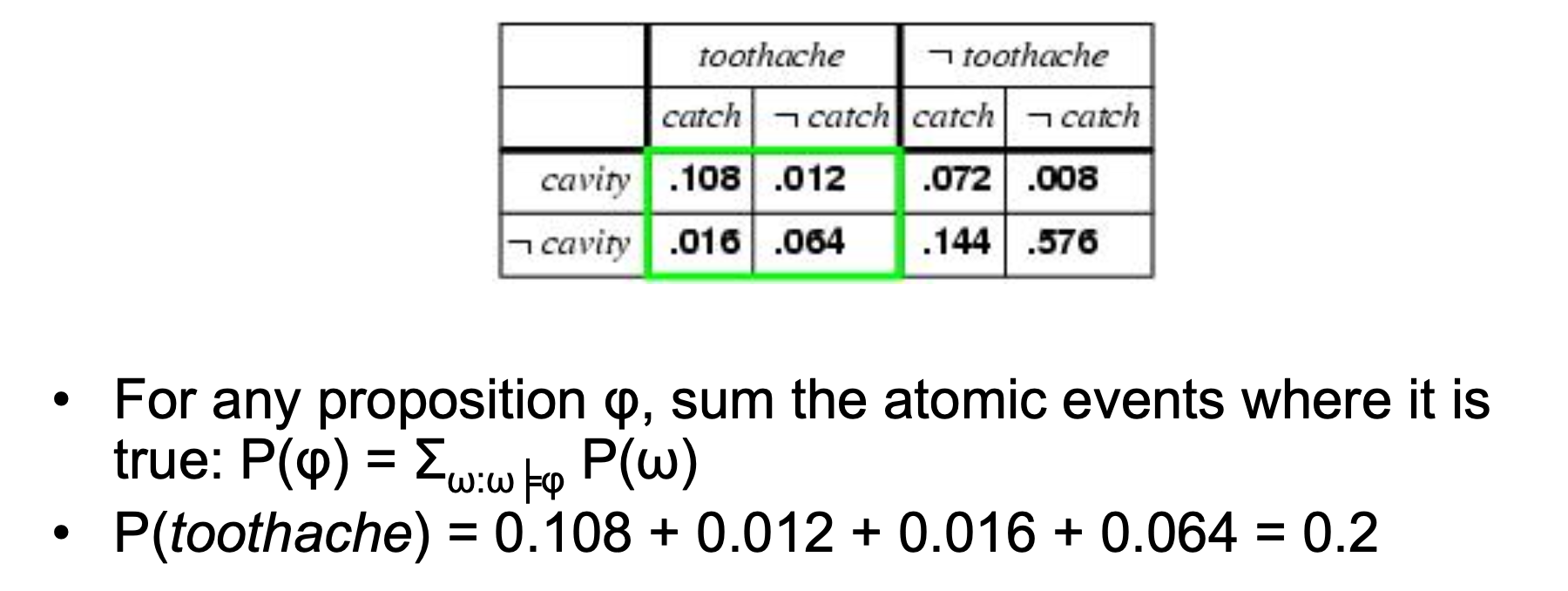
그리고 P(Cavity=True | Toothache=True)
와 같은 조건부 확률은 어떻게 구하면 될까? 직접 구해보자
p_up = enumerate_joint(variables, evidence, full_joint)
p_down = enumerate_joint(variables, evidence, full_joint)
print(p_up / p_down)
이렇게 우리는 치통이 있다는 증거가 주어졌을 때 충치의 확률을 구할 수 있었다. 그렇다면 치통이 있다는 증거가 주어졌을 때 충치가 '없을' 확률은 어떻게 구할 수 있을까? 이는 P(toothace = True) 가 분모에 있음을 주목하여 정규화를 활용하면 된다.

psource(enumerate_joint_ask)
def enumerate_joint_ask(X, e, P):
"""
[Section 13.3]
Return a probability distribution over the values of the variable X,
given the {var:val} observations e, in the JointProbDist P.
>>> P = JointProbDist(['X', 'Y'])
>>> P[0,0] = 0.25; P[0,1] = 0.5; P[1,1] = P[2,1] = 0.125
>>> enumerate_joint_ask('X', dict(Y=1), P).show_approx()
'0: 0.667, 1: 0.167, 2: 0.167'
"""
assert X not in e, "Query variable must be distinct from evidence"
Q = ProbDist(X) # probability distribution for X, initially empty
Y = [v for v in P.variables if v != X and v not in e] # hidden variables.
for xi in P.values(X):
Q[xi] = enumerate_joint(Y, extend(e, X, xi), P)
return Q.normalize()
함수를 활용해서 P(Cavity | Toothache=True) 은 어떻게 구할 수 있을까?
query_var = 'Cavity'
evidence = dict(toothache = True)
ans = enumerate_joint_ask(query_var, evidence, fill_joint)
(ans[True], ans[False])
4. 베이즈망
결합 확률 분포를 효과적으로 표현하기 위한 베이즈망을 코드로 구현해본다.
여기서 베이즈망는 BayesNet이라는 클래스를 통해서 구현된다. 이는 우선 BayesNode라는 클래스를 통해서 구현된 node들을 포함하고 있다. 각 노드들은 하나의 확률 변수에 대응되며 조건부 확률표(CTP)를 포함해야한다. (조건부 확률표는 각 노드에 연관된 국소 확률 정보를 의미한다)
psource(BayesNode)class BayesNode:
"""A conditional probability distribution for a boolean variable,
P(X | parents). Part of a BayesNet."""
def __init__(self, X, parents, cpt):
"""X is a variable name, and parents a sequence of variable
names or a space-separated string. cpt, the conditional
probability table, takes one of these forms:
* A number, the unconditional probability P(X=true). You can
use this form when there are no parents.
* A dict {v: p, ...}, the conditional probability distribution
P(X=true | parent=v) = p. When there's just one parent.
* A dict {(v1, v2, ...): p, ...}, the distribution P(X=true |
parent1=v1, parent2=v2, ...) = p. Each key must have as many
values as there are parents. You can use this form always;
the first two are just conveniences.
In all cases the probability of X being false is left implicit,
since it follows from P(X=true).
>>> X = BayesNode('X', '', 0.2)
>>> Y = BayesNode('Y', 'P', {T: 0.2, F: 0.7})
>>> Z = BayesNode('Z', 'P Q',
... {(T, T): 0.2, (T, F): 0.3, (F, T): 0.5, (F, F): 0.7})
"""
if isinstance(parents, str):
parents = parents.split()
# We store the table always in the third form above.
if isinstance(cpt, (float, int)): # no parents, 0-tuple
cpt = {(): cpt}
elif isinstance(cpt, dict):
# one parent, 1-tuple
if cpt and isinstance(list(cpt.keys())[0], bool):
cpt = {(v,): p for v, p in cpt.items()}
assert isinstance(cpt, dict)
for vs, p in cpt.items():
assert isinstance(vs, tuple) and len(vs) == len(parents)
assert all(isinstance(v, bool) for v in vs)
assert 0 <= p <= 1
self.variable = X
self.parents = parents
self.cpt = cpt
self.children = []
def p(self, value, event):
"""Return the conditional probability
P(X=value | parents=parent_values), where parent_values
are the values of parents in event. (event must assign each
parent a value.)
>>> bn = BayesNode('X', 'Burglary', {T: 0.2, F: 0.625})
>>> bn.p(False, {'Burglary': False, 'Earthquake': True})
0.375"""
assert isinstance(value, bool)
ptrue = self.cpt[event_values(event, self.parents)]
return ptrue if value else 1 - ptrue
def sample(self, event):
"""Sample from the distribution for this variable conditioned
on event's values for parent_variables. That is, return True/False
at random according with the conditional probability given the
parents."""
return probability(self.p(True, event))
def __repr__(self):
return repr((self.variable, ' '.join(self.parents)))생성자에는 variable, parents 그리고 cpt 가 정의되어야 한다. variable 에는 지진과 같은 변수의 이름이 들어가야하고, parents 에는 부모 노드의 리스트(혹은 ' '로 분리된 문자열)가 정의되어야 한다. 조건부 확률표(cpt)에는 {(v1, v2, ...): p, ...}와 같은 딕셔너리 형태로 정의되어야 한다.
이를 강의에서 다룬 예제로 살펴보자.
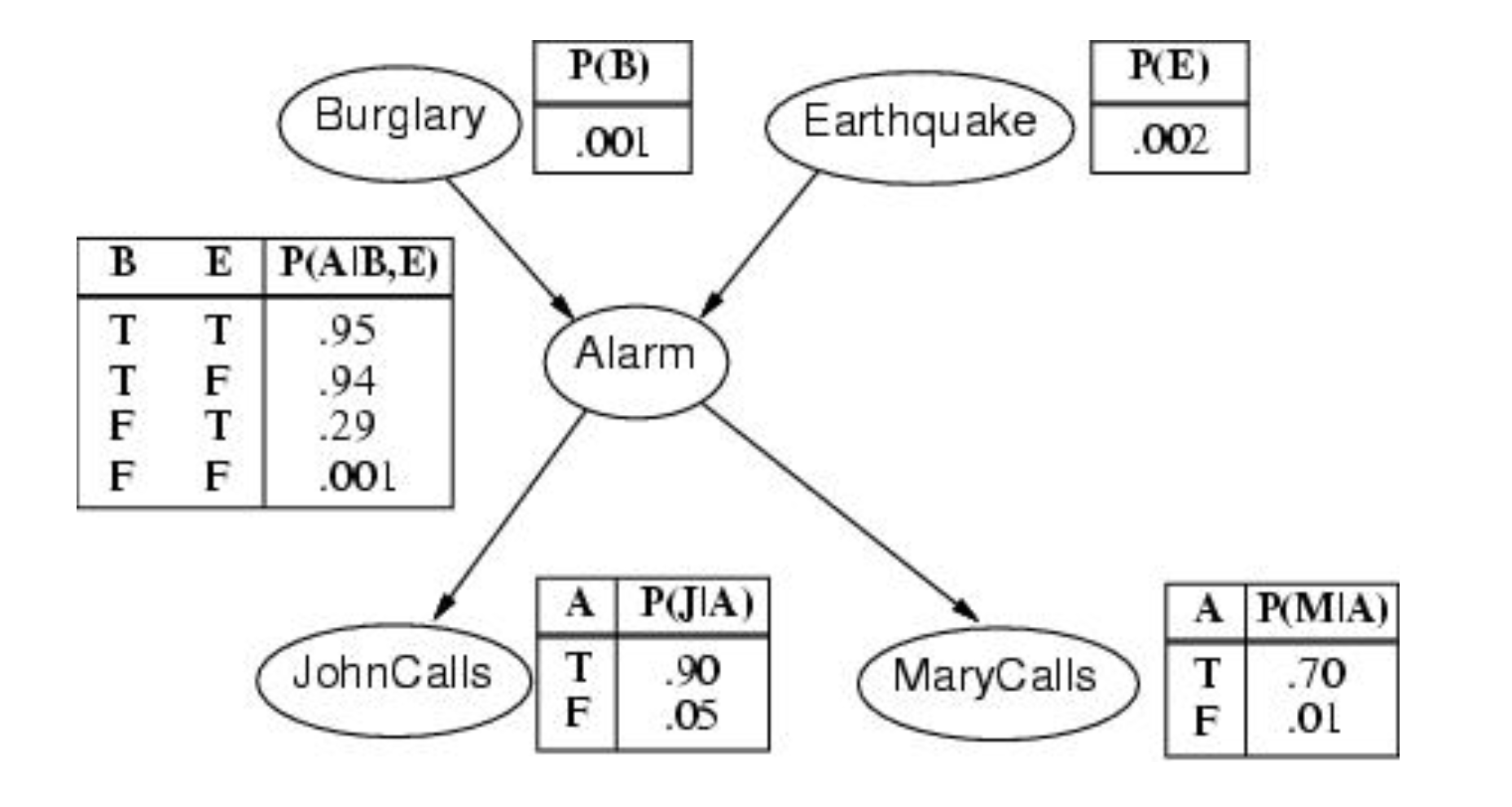
여기서 alarm 노드를 하나의 예시로 구현하면 아래와 같다.
alarm_node = BayesNode('Alarm', ['Burglary', 'Earthquake'],
{(True, True): 0.95,(True, False): 0.94, (False, True): 0.29, (False, False): 0.001})
john_node = BayesNode('JohnCalls', ['Alarm'], {True: 0.90, False: 0.05})
mary_node = BayesNode('MaryCalls', 'Alarm', {(True, ): 0.70, (False, ): 0.01}) # Using string for parents.
# Equivalant to john_node definition.
부모 노드가 없을 때는 다음과 같이 정의하면 된다.
burglary_node = BayesNode('Burglary', '', 0.001)
earthquake_node = BayesNode('Earthquake', '', 0.002)
각 노드의 조건부 확률은 p 메서드를 통해 확인할 수 있다. value 와 event 를 입력으로 한다. 이때 event 는 {변수 : 값} 형태의 딕셔너리여야 한다. 최종적으로는 P(X=value | parents=parent_values) 라는 조건부 확률을 반환한다.

때에 따라서 하나의 네트워크에 노드를 추가해야하는 경우가 있다. BayesNode에서는 노드들을 모두 정의하여 이를 구현하였지만 BayesNet에서는 하나의 클래스에서 바로 이를 정의하고 노드들을 추가할 수있습니다.
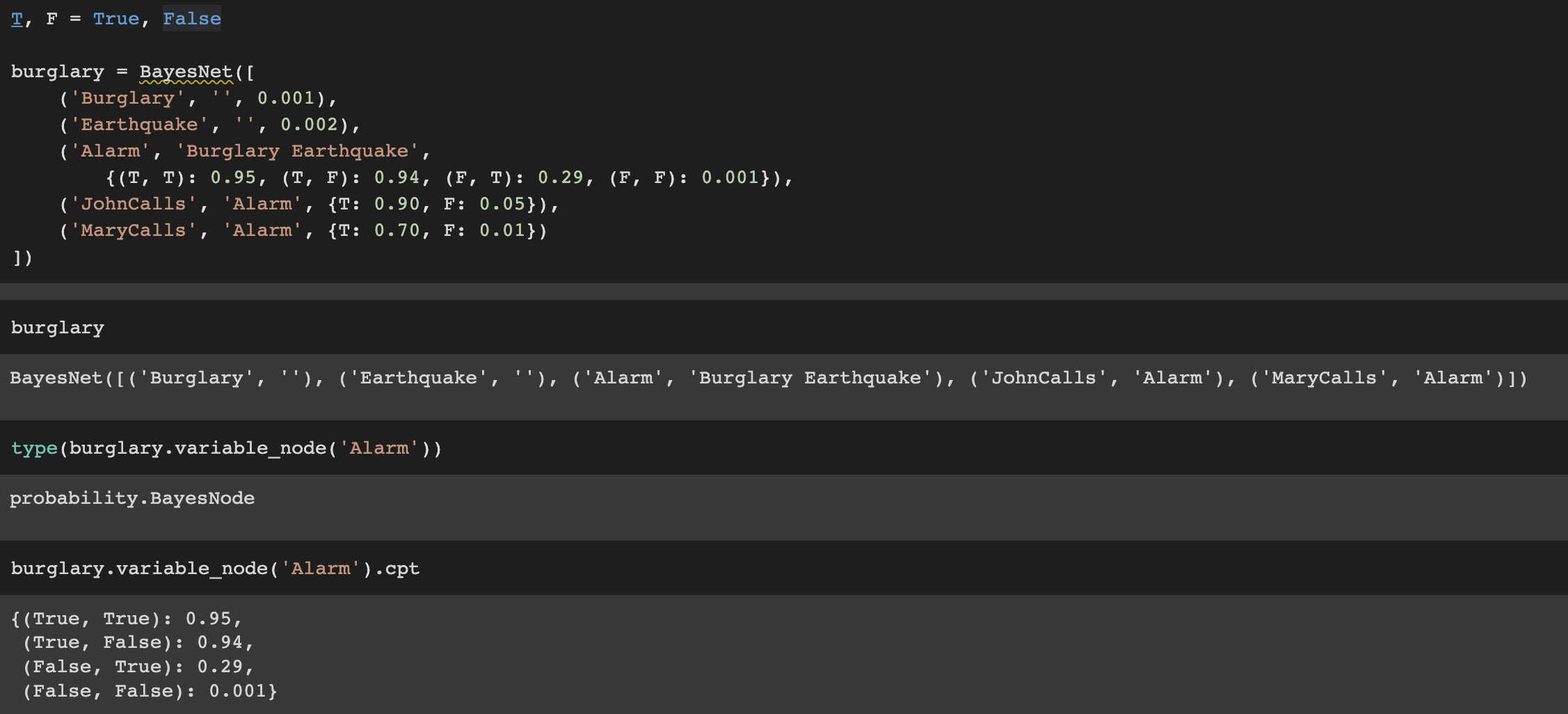
(강의 자료에는 아래 자료가 포함되어 있지 않음. 일단 실습 수업시간에는 진행함)
5. 베이즈망의 정확 추론
베이즈망은 완전 결합 확률의 간결한 표현이다. 그래서 완전 결합 확률을 활용해서 추론을 진행한 것 처럼 베이즈망을 통해서도 추론을 진행할 것이다. 이번 시간에는 추론 중에서도 근사 추론이 아닌 정확 추론 을 다루어 볼 것이며 열거에 의한 추론 을 살펴볼 것이다. (아마 수업시간에는 진행하지 않았을 것이다.)
psource(enumerate_all)def enumerate_all(variables, e, bn):
"""Return the sum of those entries in P(variables | e{others})
consistent with e, where P is the joint distribution represented
by bn, and e{others} means e restricted to bn's other variables
(the ones other than variables). Parents must precede children in variables."""
if not variables:
return 1.0
Y, rest = variables[0], variables[1:]
Ynode = bn.variable_node(Y)
if Y in e:
return Ynode.p(e[Y], e) * enumerate_all(rest, e, bn)
else:
return sum(Ynode.p(y, e) * enumerate_all(rest, extend(e, Y, y), bn)
for y in bn.variable_values(Y))해당 수식은 3. 완전 결합 분포를 활용한 추론에서 봤던 것 처럼 추론을 위한 수식이다. 이를 더욱 간단하게 구현한 것이 아래와 같은 함수들이다.
psource(enumeration_ask)def enumeration_ask(X, e, bn):
"""
[Figure 14.9]
Return the conditional probability distribution of variable X
given evidence e, from BayesNet bn.
>>> enumeration_ask('Burglary', dict(JohnCalls=T, MaryCalls=T), burglary
... ).show_approx()
'False: 0.716, True: 0.284'"""
assert X not in e, "Query variable must be distinct from evidence"
Q = ProbDist(X)
for xi in bn.variable_values(X):
Q[xi] = enumerate_all(bn.variables, extend(e, X, xi), bn)
return Q.normalize()
이 함수들을 사용하여 P(Burglary=True | JohnCalls=True, MaryCalls=True) 를 burglary 를 이용하여 풀 수 있다. 이때 X = 변수명, e = 증거({'Alarm': True, 'Burglary': True}와 같은 딕셔너리 형태), bn = 베이즈망 이다. 직접 코드를 짜고 결과를 출력해보자.
query_var = 'Burglary'
evidence = dict(JohnCalls = True, MaryCalls = True)
ans = enumeration_ask(query_var, evidence, burglary)
(ans[True], ans[False])'2023 > 2023-1' 카테고리의 다른 글
| [캡스톤 디자인] 4월 5일(수) 회의록 (0) | 2023.04.05 |
|---|---|
| [4월4일(화)] 인공지능 입문(이론) - Introduction to Machine Learning (0) | 2023.04.04 |
| [캡스톤디자인] 제안서 발표 피드백 정리 (0) | 2023.03.24 |
| [3/23(목)] 인공지능 입문(실습) - 명제 지식 베이스, 추론, CNF (0) | 2023.03.23 |
| [3/21(화)] 인공지능 입문(이론) - 명제 지식 베이스, 진리표(과제 있음) (0) | 2023.03.21 |