컴퓨터 구성 (1주차 2강 정리자료)
1장 - 디지털 논리 회로(Digital Logic Circuit)
1-1 Digital Computer : 디지털 컴퓨터가 무엇인가?
1-2 Logic Gates : 디지털 컴퓨터는 디지털 시스템이고, 모든 디지털 시스템의 구성 요소는 논리 소자이다. 회로 자체가 논리 소자로 만들어지기 때문에. 그리고 1-1 파트에서는 몇 가지의 논리 소자 소개를 해주실 예정
ex) And Gate, Or Gate, Not Gate
1-3 Boolean Algebra : 우리말로 이진 대수식, 이진 대수식을 이용해 회로를 표현할 수 있음
또한, 이진 대수식을 이용해서 회로를 간소화 시킬 수 있음.
1-4 Map Simplification : 회로를 간소화 시키는 또 다른 방법 = "맵 간소화 방법"
1-5 Combinational Circuits : 원하는 대로 동작을 하는 회로를 어떻게 설계하는지, 그래서 먼저 배울 회로
조합회로이다. 조합회로의 동작 방식은 입력값이 주어지는 즉시 Delay없이 출력값이 나오는 방식
대표적인 예) 투표, 예를 들어 5명이 투표를 한다고 생각하고 찬성은 손을 들고, 반대는 가만히 있는 다고 생각해보면 입력변수는 5가 된다. 그 중에 3명이 손을 든다면, 과반수가 넘어 전체 찬성이 된다. 그러나 2개 이하의 손이 올라온다면 반대처리가 된다. 이런식으로 시작과 동시에 결과를 알 수 있는 회로를 조합회로 라고 한다.
1-6 Flip-Flops : 1000비트의 기억소자, 우리가 만약 8비트 짜리 정보를 저장하고 싶다면?
Flip-Flops 8개를 이어붙여 8비트의 정보를 저장할 수 있다.
(+ 조합회로가 합쳐진다면 순차회로를 설계할 수 있다)
1-7 Sequentail Circuits : 순차 회로는 조합 회로와 다르게 입력값이 순차적으로 한 번에 한 개씩 들어온다.
ex) 자판기를 생각해볼 수 있다. 자판기에서 300원짜리 음료를 마신다고 하면 100원 짜리 동전 3개를 순차적으로
넣어야한다. 이렇게 순차적으로 입력값이 발생한 후, 입력값이 모두 끝난 후 출력값이 나오는 회로를 순차 회로.
1.1 디지털 컴퓨터
◎ 디지털 컴퓨터
- 여러가지 계산을 수행하는 디지털 시스템
- 0/1만을 이용하는 2진수 시스템 : 0/1 이들 각각을 비트라고 칭한다.(Binary Information digiT)]
- 컴퓨터 내부의 정보가 제한된 수의 불연속적 값으로 표시
◎ 디지털 시스템
- 전자 부품의 물리적 제약과 인간의 논리적 2진적(T,F)이라는 이유대문에 오직 2개의 값만을 가지도록 제한
◎ 우리는 2진수를 이용해 정보를 표현할 수 있다
2진수 숫자는 각 자리수마다 가중치를 가지고 있다.
◎ 컴퓨터의 구분 : 크게 하드웨어, 소프트웨어로 구분 가능
- 하드웨어 : 컴퓨터의 모든 전자부품과 주변장치를 구성하는 전자기적 부품 (눈에 보이는 것)
- 소프트웨어 : 컴퓨터의 정보처리 작업을 수행하는 명렁어와 데이터로 구성 (눈에 보이지 않는 것)
< 시스템적 입장에서의 구분 >
◎ 시스템 소프트웨어 (운영체제)
- 컴퓨터의 시스템을 효율적으로 사용하기 위한 목적을 가진 프로그램(Compiler)
- 사용자가 요구하는 하드웨어 기능간의 차이점을 보상
◎ 하드웨어
▶ 중앙 처리 장치(Centeral Processing) CPU
-데이터를 조작하는 산술 및 논리연산 부분
-데이터를 저장하고 가공한 후 임시로 저장하는 레지스터(Register) ; CPU가 직접 가지고 있는 기억소자
-명령어를 가져와 수행하는 제어회로
▶ 기억장치(Random Access Memory) : 명령어 또는 데이터 저장
▶ 입출력 장치
- 컴퓨터와 외부 세계와의 통신과 데이터 전송을 제어
ex) 키보드, 프린터, 터미널, 디스크

★ 우선은 입력 장치로 입력을 받아 처리를 해주는 Input&Output Processer 또는 디바이스의 컨트롤러에서 받아
CPU로 전달하는데, 그 전에 RAM에 간 후 CPU로 전달된다. 출력도 마찬가지로 CPU가 명령어를 내리고 그게 RAM을 거쳐 다시 출력 장치를 통해 출력값이 생성된다.
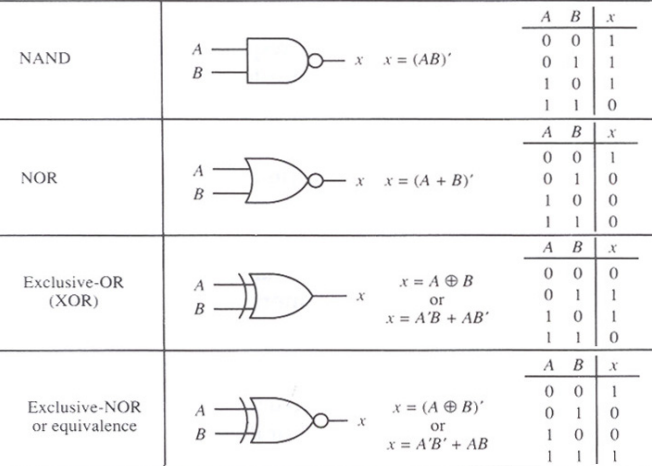
1.2 Logic Gates
< 8개의 논리 소자 >

▶ NAND는 출력 단자에 AND와 달리 동그라미가 하나 붙어있는데 그게 NOT게이트의 점이다.
NAND와 정확히 반대로 행동(출력값이 0이 나오는 경우는 정보 표현이 둘 다 1일 경우)
▶ NOR는 OR게이트 출력에 NOT 게이트가 붙은 것 ; OR게이트이 정반대로 행동
▶ XOR게이트는 두 개의 입력 변수값이 서로 다른 경우에만 1을 출력
▶ XNOR게이트는 XOR와 정반대 ; 입력값이 모두 같을 때만 1을 출력
가장 중요한 논리 소자는 AND, OR, NOT게이트! 다른 것은 저 3개의 논리 소자로 모두 만들 수 있음

1-3 Boolean Algebra
▶ 구성 요소 : 이진 변수와 logic operation(AND,OR,NOT...)
▶ F(x, y, z) = x +y'z
-> x라는 이진변수 y라는 이진변수 z라는 이진변수를 사용하는 Function는 x 또는 y'z라고 정의된다.
x와 y'z는 OR로 묶여있고, y'z는 AND게이트, y는 NOT게이트

-> 출력값이 1이 되는 경우는
① x값이 1
② y값이 0, z값이 1
위처럼 동작하는 회로는 1개가 아님. 여러개가 있을 수 있으나, 중요한건 어떤 회로가 가장 간소화된 회로인지가 중요
◎ Boolean 대수식을 사용하면,
- 변수사이의 진리표 관계를 대수식 형태로 표시
- 논리 회로도의 입출력 관계를 대수식 형태로 표시
- 같은 기능을 가진 더 간단한(간소화된) 회로 발견
< 중요한 관계도 >

(15), (16)번은 드 모르간의 정리라고 불림, (14)번은 염두에 두고 있어야 나중에 실수를 줄이고, 회로를 간소화 시키는데 도움이 됨
◎ 드 모르간의 정리
- 어떤 수식에서 모든 OR연산은 AND로, AND연산은 OR로 바꾸어 주고 각 변수를 보수화
ex) F = AB + C'D' B'D
F' = (AB + C'D' + B'D)' = (AB)' · (C'D')' · (B'D)' = (A'+B')(C+D)(B+D')
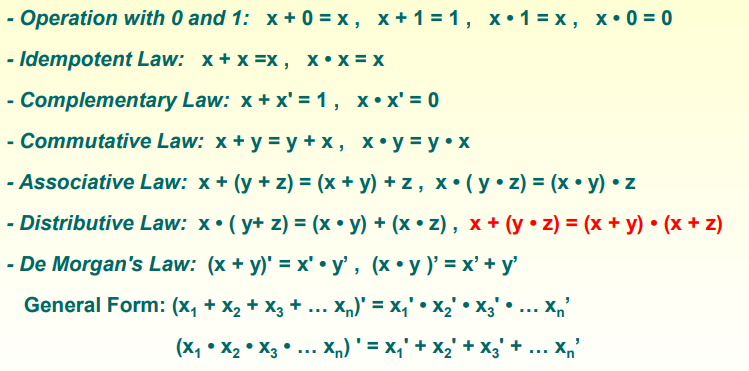

AND 게이트는 3개가 필요
그리고 다 출력을 묶어줄 OR게이트 필요
그리고 NOT게이트 2개 필요
-> 위의 그림이 아무런 단순화 작업을 하지 않았을 때 회로도
식의 간소화 과정을 거쳐 나온 회로도가 아래 회로도, 아까도 강조했던 것처럼 같은 결과를 출력하겠지만 중요한 것은 최대한 간소화 작업을 거치는 게 중요
