오늘 배울 내용은 1-5 Combinational Circuits : 조합회로
우리가 배울 회로는 2가지가 존재한다. 하나는 조합회로, 또 다른 회로는 순차회로이다.
이 두 가지 회로의 차이점
조합 회로는 말 그대로 조합회로이다. 이 경우에는 어떤 입력 변수들의 값이 들어오는 즉시 출력값이 바로 결정이 된다.
여러 논리 소자들을 통과하면서 우리가 원하는 출력값이 나오도록 동작을 하는 회로이다. 그 경우에 중간에 있는 논리소자들을 통과하는 시간이 매우 작기 때문에 무시 할 수 있다. ex) 선거
순차 회로는 1비트 짜리 정보를 저장하는 기억 소자가 조합 회로와 같이 합쳐져 순차 회로를 만들어낸다.
ex) 자판기, 가격에 맞는 돈이 들어올 때까지 그 돈이 저장되어있다가 가격을 만족하면 버튼에 불이 들어와 버튼을 누르면 음료가 나오는 과정
설계 전에 분석을 진행 -> 주어진 회로가 어떻게 작동되는지 분석하고 결과가 boolean 함수 또는 Truth table인지 분석
우리가 많이 진행하는 것은 설계!
설계하는 단계
1. 문제를 이해한다. (무엇을 위한 회로인가)
2. 각각의 입출력 변수들의 이름을 결정해준다
3. Truth Table을 결정해준다.
4. 3번 결과물을 이용하여 K-map 또는 Boolean대수를 이용하여 간소화 시킨다.
K-map의 장점은 하라는 대로만 하면 결과값이 가장 간소화를 보장함
5. 간소화한 논리 회로를 그린다.
▶ Design Example : Half Adder
Half Adder는 조합 회로이다. 산술적인 더하기를 진행하는데 1비트 짜리 2개의 입력값을 받아 서로 더한다.
x,y 입력값이 주어질 떄 더했을 때 값을 Sum, Carry는 올림수 값

▶ 또 다른 예 Full Adder
-> 조합회로인데, 3개의 입력값들을 서로 더한다. (Carry값도 같이 고려한다)
입력값은 3개, 출력값은 아까와 동일하게 2개(S, C)
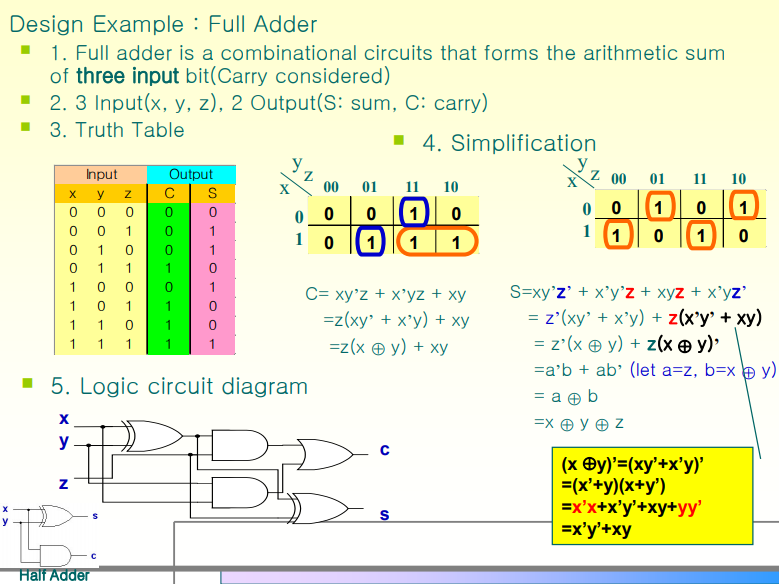
C그림의 파란색 부분 2개가 그룹핑 되어있는데 전 시간에 배운 그룹핑 방법과는 다르다. 그 이유는 Full Adder는 Half Adder 2개를 구성해서 만들 수 있기 때문. 하나의 민텀은 더 이상 간소화가 어렵기 때문에 바로 수식을 작성하면 된다.
S map 그림도 보면 빨간색 부분 4개가 독립적으로 민텀이 형성되어있다. 간소화를 더 이상 진핼 할 수 없기에 바로 수식으로 작성해주면 된다.
그림을 보면 Half Adder 2개를 이용해 Full Adder 만들 수 있다-> Full Adder는 Half Adder2개로 구성할 수 있다
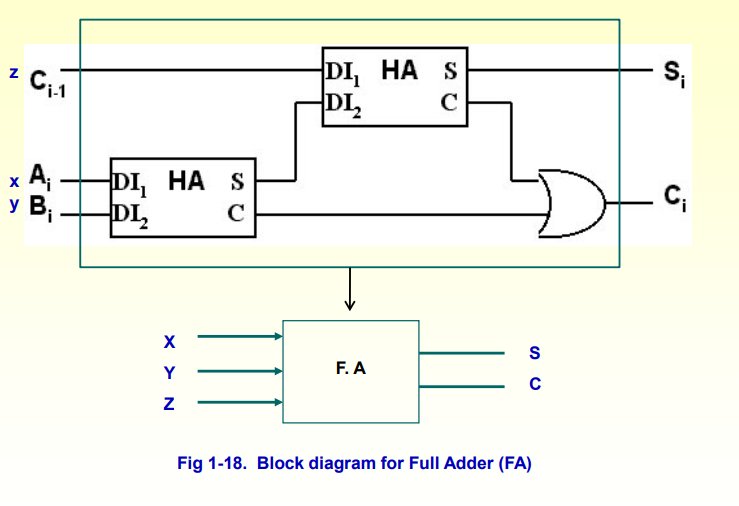

1. 3개의 입력값이 라는 조건이 있기에 경우의 수는 2^3 = 8가지가 존재한다 (오른쪽 위 그림)
2. 테이블을 그려놓고, 결과값을 확인한다. 문제 설명에 적은 조건대로 결과값 작성(Truth Table)
3. 이제 간소화를 진행한다 (K-Map이용), 그룹핑 진행 : F= AC + BC + AB
4. 간소화를 통해 알아낸 함수식을 논리회로도로 그려준다.
5. Truth Table에서 출력값이 1인 논리식을 하나 회로도에 적용시켜본다 (위 사진에서는 빨간색 칸에 해당됨)
1-6 : Flip-Flops : 1비트짜리 기억소자
조합 회로 : 논리 소자로만 구성됨, 그러나
순차 회로 : 논리 소자 + Filp-Flops
우리는 4개의 Flip-Flops을 배움
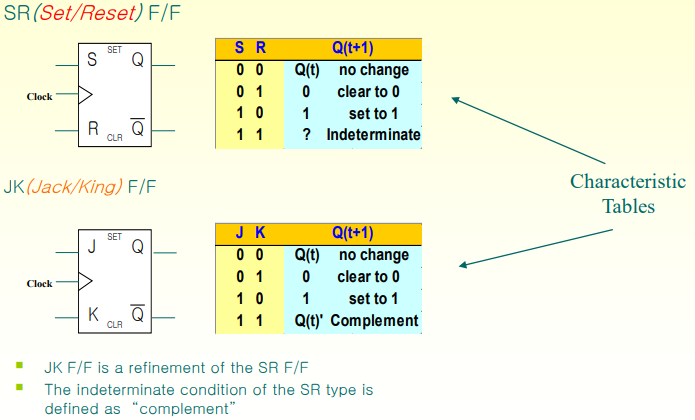
SR F/F
입력 단자 3개 : S단자, R단자, Clock신호
출력 단자 2개 :
Q단자 : Flip-Flops안에 들어있는 값을 그대로 내보냄
Q_Bar단자 : Flip-Flops값에 들어가 있는 입력 값의 역함수 값
CLR단자 : CLR단자에 값이 들어가면 Flip-Flops값이 모두 0으로 초기화
Set단자 : Set단자에 값이 들어가면 Flip-Flops값이 모두 1로 초기화
Q(t+1) : SR F/F의 다음상태를 나타냄
Q(t) : SR F/F의 현상태를 나타냄
-> 그림을 보면 Q(t)가 존재하면 다음 Q(t+1)의 변화는 없고, Q(t)가 0이면 Q(t+1)도 0으로 초기화,
Q(t)가 1이면 1로 설정, Q(t)가 ?이면 Q(t+1)도 결정되지 않는다
JK F/F : 이해하기 쉽게 보자면 J단자는 Set단자, K단자는 Reset단자
SR F/F와의 다른 점은 J/K단자 모두 1이 들어오면 Q(t+1)은 Q(t)의 Complement가 된다 (현상태 0-> 다음상태1)
SR F/F와 JK F/F의 차이점은 위 1가지 외엔 비슷함
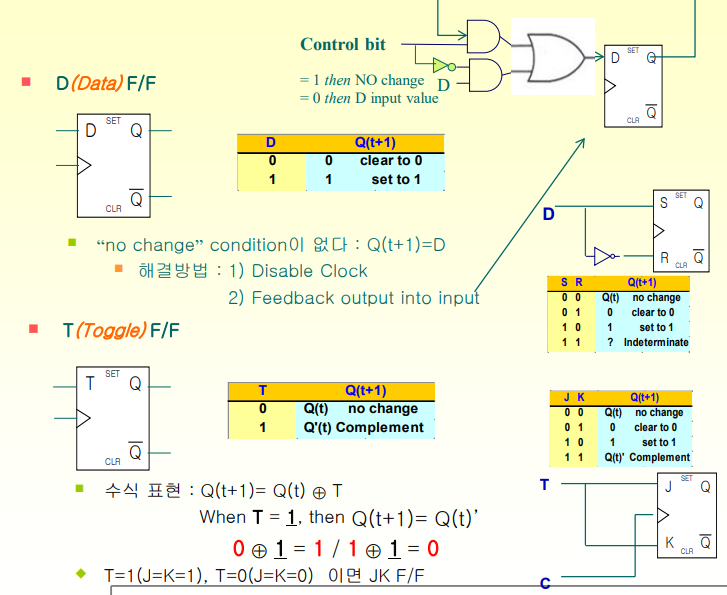
D F/F : 입력 단자가 1개만 있음 (Clock단자 제외)
D단자에 0이 들어오면 다음 상태 0
D단자에 1이 들어오면 다음 상태 1
위 단자의 문제는 "no change" condition이 없다. 해결방법은 Clock단자에 신호가 들어오지 않도록 한다. 두번째 방법은 출력값을 뒤로 돌려 다시 입력으로 넣어준다. 위 그림 오른쪽 맨 위 그림. D에 들어왔을 때 출력값을 뒤로 돌려 다시 입력 값을 넣어줌 (강의 42분 ~)
T F/F : T단자에 0이 들어오면 다음 상태는 현상태 값 그대로, 1이 들어오면 다음 상태는 현재 상태의 Complement
JK F/F을 이용해서도 T F/F처럼 동작하게 만들 수 있다. T F/F 대신 JK F/F/가능
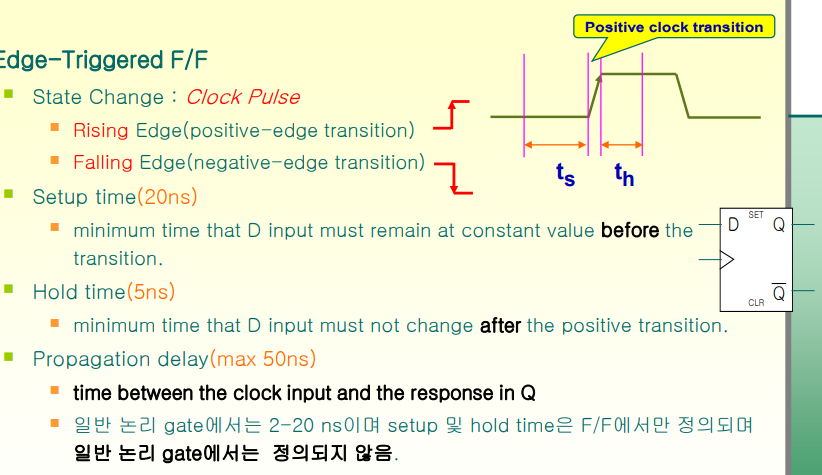
Clock 신호 : 똑같은 주기를 가지고 같은 신호를 반복
F/F는 Clock신호에 맞춰 동기화되는데,
Clock값이 위로 튈 때 F/F값이 바뀐다. -> Rising Edge
Clock값이 밑으로 튈 때 F/F값이 바뀐다 -> Falling Edge
F/F은 Setup Time은 위 그림의 ts -> 만약 D F/F를 사용하고 있다고 하면 D단자로 들어온 값은 Setup time에 해당되는
(20ns)만큼 같은 신호값이 유지가 되어야 한다. 역시 마찬가지로 상태가 변화가 이루어진 이후에 D input값은 Hold Time(5ns)만큼 변화가 없어야 한다. Setup time과 Hold time은 똑같이 상태의 변화가 존재하지 않지만 Positive clock transition을 기준으로 둔다.
-> Setup/Hold time은 Flip-Flops에서만 정의된다. 일반적인 논리 회로에서는 정의되지 않음
Propagation delay라고 하는 것은 이제 F/F이 동작이 시작했을 때, 그렇게 되어서 이 안에 상태값이 바뀔 때까지 그 떄까지 걸리는 시간이라고 칭함
-> 일반적으로 논리 회로에서도 존재
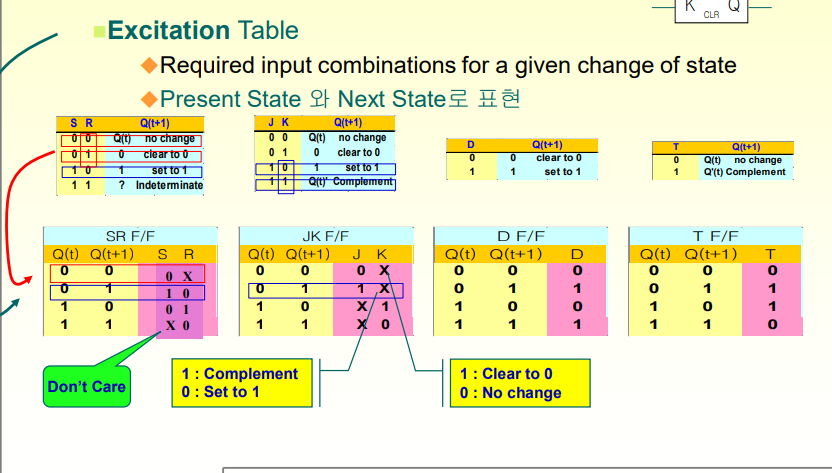
일반적으로 우리가 순차회로를 설계할 때, 어떤 값들을 J단자 K단자에 물려주어야 우리가 원하는 상태 변화를 이끌어낼 수 있나 라는게 궁금할 때, 사용하는 것이 Next State
Don't Care은 간소화 시킬 수 있으면 1로 사용하고, 그 경우가 아니라면 0으로 버린다. 그렇기 떄문에
Don't Care가 많이 들어가 있는 F/F을 사용하는게 회로를 간소화 시키는 입장에서 더 도움이 된다.
만약 어떤 F/F을 사용하라고 명시 되어있지 않으면 일단은 JK를 사용하는게 유리하다. (Don't Care가 많기 때문에)