https://www.acmicpc.net/problem/2565
2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
문제
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.
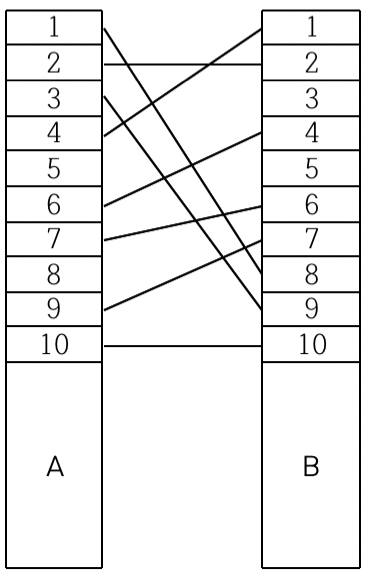
< 그림 1 >
전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
출력
첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
주어진 전깃줄을 연결했을 때 서로 교차하지 않도록 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 문제.
이 문제 유형은 대표적인 가장 긴 증가하는 부분 순열을 이용하는 문제이다.
왼쪽 전봇대에 연결된 전깃줄을 기준으로 오름차순 정렬한 후, 오른쪽 전봇대에 연결된 전깃줄로 가장 긴 증가하는 부분 수열 값을 구해 가장 큰 수를 연결된 전깃줄에서 뺀 값이 없애야 할 전깃줄의 개수이다.
왼쪽 수들은 어처피 정렬되어있고 오른쪽 수들 중 가장 긴 증가하는 부분 순열로 해당되는 수들은 모두 겹칠리 없기 때문이다.
하지만 이 문제에는 해당되지 않지만 하나 보고 가야할 것이 같은 위치에 전깃줄을 놓을 수 있는지이다
예를 들면 전깃줄이 총 5개가 있고
1 2
2 3
3 3
4 5
5 1
이라고 하면, 위 예시는 같은 위치 3에 전깃줄이 2개가 놓여진 것이다.
이때에는 5 1 하나만 없애도 모두 교차하지 않는다. 그렇기 때문에 증가하는 부분 순열이 아닌 증거하면서 같을수도 있는 경우가 된다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
using namespace std;
struct node {
int from;
int to;
};
struct node line[101];
int a[101];
bool compare(struct node a, struct node b) {
if (a.from == b.from) {
return a.to < b.to;
}
else {
return a.from < b.from;
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n;
cin >> n;
for (int i = 0; i < n; i++) {
a[i] = 1;
cin >> line[i].from >> line[i].to;
}
sort(line, line + n, compare);
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
if (line[j].to < line[i].to) {
a[i] = max(a[i], a[j] + 1);
}
}
}
int answer = *max_element(a, a + n);
cout << n - answer << '\n';
return 0;
}'BOJ > DP' 카테고리의 다른 글
| [C/C++] 백준 - 12865번 : 평범한 배낭 (0) | 2021.07.10 |
|---|---|
| [C/C++] 백준 - 10844번 : 쉬운 계단 수 (0) | 2021.07.09 |
| [C/C++] 백준 - 1904번 (01타일) (0) | 2021.07.04 |
| [C/C++] 백준 - 1003번 (피보나치 함수) (0) | 2021.07.04 |
| [C/C++] 백준 - 1912번 (연속합) (0) | 2021.07.02 |